![[Delta r]](../thgif/Deltar.gif) G 'o
G 'o![[Delta r]](../thgif/Deltar.gif) H 'o
H 'o![[Delta r]](../thgif/Deltar.gif) S 'o
S 'o
Contents of Section
4.2 Recommendations concerning biochemical reactions
4.3 The importance of distinguishing between chemical equations and biochemical equations
4.4 Experimental matters
References for this Section
When pH and pMg are specified, a whole new set of transformed thermodynamic properties come into play (ref. 4, 5). These properties are different from the usual Gibbs energy G, enthalpy H, entropy S, and heat capacity at constant pressure CP, and they are referred to as the transformed Gibbs energy ![[Delta r]](../thgif/Deltar.gif) G 'o
G 'o![[Delta r]](../thgif/Deltar.gif) H 'o
H 'o![[Delta r]](../thgif/Deltar.gif) S 'o
S 'o
G 'o =
H 'o - T
S 'o . . . . . . . . (26)
The standard transformed enthalpy of reaction is given by
. . . . . . . . (27)
If ![[Delta r]](../thgif/Deltar.gif) H 'o is independent of temperature in the range considered, it can be calculated using
H 'o is independent of temperature in the range considered, it can be calculated using
H 'o = [RT1T2/(T2 - T1)] ln (K2'/K1') . . . . . . . . (28)
where K2' and K1' are measured at the same P, pH, pMg, and I. If ![[Delta r]](../thgif/Deltar.gif) H 'o
H 'o![[Delta r]](../thgif/Deltar.gif) CP'o
CP'o
H 'o(T) =
H 'o(298.15 K) + (T - 298.15 K)
CP'o . . . . . . . . (29)
This more complicated equation is analogous to equation 16. The standard transformed reaction entropy can be calculated from the standard transformed molar entropies of the reacting species:
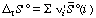 , where the
, where the i' are the apparent stoichiometric numbers (positive for products and negative for reactants) of the reactants i in a biochemical reaction written in terms of reactants (sums of species) (for example, reaction 6).
The standard transformed enthalpy of reaction ![[Delta r]](../thgif/Deltar.gif) H 'o can also be calculated from calorimetric measurements. When that is done it is necessary to make corrections for the enthalpies of reaction caused by the change
H 'o can also be calculated from calorimetric measurements. When that is done it is necessary to make corrections for the enthalpies of reaction caused by the change ![[Delta r]](../thgif/Deltar.gif) N(H+)
N(H+)![[Delta r]](../thgif/Deltar.gif) N (Mg2+)
N (Mg2+)![[Delta r]](../thgif/Deltar.gif) N (H+)
N (H+)![[Delta r]](../thgif/Deltar.gif) N(Mg2+)
N(Mg2+)
The change in binding of H+ and Mg2+ in a biochemical reaction can be calculated if the acid dissociation constants and magnesium complex dissociation constants for the reactants are known; the equilibrium constant for the biochemical reaction itself does not have to be known for this calculation. Earlier calculations of the production of H+ and Mg2+ used a different sign convention (ref. 9). The changes in binding ![[Delta r]](../thgif/Deltar.gif) N(H+)
N(H+)![[Delta r]](../thgif/Deltar.gif) N(Mg2+)
N(Mg2+)
N(H+) =
![[Sigma]](../../greek/SSIGMA.GIF)
i'
H(i ) . . . . . . . . (30)
where the
where the logarithms are log10. A pHstat can be used to measure
Since the standard transformed thermodynamic properties
where Q ' is the apparent reaction quotient of specified concentrations of reactants (sums of species). The change in transformed Gibbs energy
The corresponding changes in transformed entropy and transformed enthalpy are given by
The calorimetrically determined enthalpy of reaction
When the pH is specified, the electromotive force of an electrochemical cell can be discussed in terms of the concentrations of reactants (sums of species) rather than species. When this is done the electromotive force of the cell or of a half cell is referred to as the apparent electromotive force
where E 'o =
Biochemists have not had the advantage of having tables of standard formation properties of reactants at some standard set of conditions involving pH and pMg. Currently, information on biochemical reactions is tabulated as standard transformed Gibbs energies of reaction
When pH and pMg are specified, the transformed formation properties (indicated by a subscript f) of reactants are defined by (ref. 4)
where the
Table III gives standard transformed enthalpies of formation and standard transformed Gibbs energies of formation that have been calculated at 298.15 K, pH = 7, pMg = 3, and I = 0.25 M (ref. 7). The values for creatine phosphate are based on the recent work of Teague and Dobson (ref. 12). The adjustment of standard formation properties of species to standard transformed formation properties at the desired pH and pMg has been mentioned in connection with Table II. When a reactant exists as a single species at pH = 7 and pMg = 3, the transformed formation properties of the species in Table II go directly into Table III. Water has to be included in this table because its formation properties must be used in equations 40 and 41, even though it does not appear in the expression for the apparent equilibrium constant. When a reactant exists at pH = 7 and pMg = 3 as an equilibrium mixture of species, isomer group thermodynamics (see Section 5.2) has to be used to calculate standard transformed formation properties (Table III) for that reactant.
Table III. Standard Transformed Formation Properties of Reactants (sums of species) at 298.15 K, pH = 7, pMg = 3, and I = 0.25 M. This table uses the convention that
The large number of significant figures in Table I might appear to indicate that these thermodynamic properties are known very accurately, but this is misleading. The values in such a table are used only by subtracting them from other values in the table, and so the only things that are important are differences between values. The values have to be given in the table with enough significant figures so that thermodynamic information in the differences is not lost. The following examples illustrate uses of this table.
This kind of table will make it easier to make thermodynamic calculations on systems of enzymatic reactions, like glycolysis. Currently, to calculate
Example 1. Calculate
ATP + Glc = ADP + Glc-6-P
= -20.89 kJ mol-1
= -30.38 kJ mol-1
Example 2. Calculate
Q ' = (10-3)(10-2)/(10-5)(10-4) = 104
Since
Note that
4.3 THE IMPORTANCE OF DISTINGUISHING BETWEEN CHEMICAL EQUATIONS AND BIOCHEMICAL EQUATIONS
Both types of equations are needed in biochemistry. Chemical equations are needed when it is important to keep track of all of the atoms and charges in a reaction, as in discussing the mechanism of chemical change. Biochemical reactions are needed to answer the question as to whether a reaction goes in the forward or backward direction at specified T, P, pH, pMg, and I, or for calculating the equilibrium extent of such a reaction. Therefore, it is essential to be able to distinguish between these two types of equations on sight. The reaction equations in Enzyme Nomenclature [ref. 13] are almost exclusively biochemical equations. In the case of the hydrolysis of adenosine triphosphate to adenosine diphosphate and inorganic phosphate, it is clear that equation 9 is a chemical equation and equation 6 is a biochemical equation. Equation 6 does not indicate that hydrogen ions or magnesium ions are conserved, but it is meant to indicate that C, O, N, and P are conserved. Equation 6 indicates the form of the expression for the apparent equilibrium constant K ' at specified T, P, pH, pMg, and I. Equation 9 indicates that electric charge is conserved, and the abbreviations ATP4- and ATP3- can be replaced by the atomic compositions of these ions to show that C, H, O, N, and P are conserved. Equation 9 indicates the form of the expression for the equilibrium constant K at specified T, P, and I. Currently, the hydrolysis of ATP is often represented by ATP + H2O = ADP + Pi + H+ in textbooks and research papers, but this is a hybrid of a chemical equation and a biochemical equation and does not have an equilibrium constant. Furthermore, this "equation" does not give the correct stoichiometry. The correct stoichiometry with respect to H+ is obtained by use of equation 32 and is
In writing biochemical equations, words are often used to avoid the implication that hydrogen atoms and charge are being balanced, but it is important to understand that all other atoms are balanced. For example,
is a biochemical equation and
is a chemical reaction. There is no unique way to write a chemical reaction; for example, this equation could be written with H2PO4- and no H+ on the right hand side. It can also be written with CO2 on the left-hand side, but then it is necessary to be clear about whether this CO2 is in the solution or gas phase. In equation 43 the word carbonate refers to the sum of the species CO2, H2CO3, HCO3-, and CO32- in aqueous solutions.
It is important to realize that K ' = K for reactions where the reactants are nonelectrolytes (ref. 14). An example is the hydrolysis of sucrose to glucose and fructose. Of course sugars do have ionizable groups, but we are usually not interested in the dissociations that occur above pH = 12. For racemases,
The need to clearly distinguish between biochemical equations and chemical equations raises problems with some abbreviations that are widely used. For example, the use of NAD+ in a biochemical equation makes it look like this charge should be balanced. NAD+ is also not a suitable abbreviation for use in a chemical equation because it is actually a negative ion.
Chemical equations and biochemical equations should not be added or subtracted from each other because their sum or difference does not lead to an equation that has an equilibrium constant. On the other hand, chemical equations can be added to chemical equations, and biochemical equations can be added to biochemical equations.
The net equation for a system of biochemical reactions can also be written as a chemical equation or a biochemical equation, but the equilibrium constants are, of course, in general different. Net equations in the form of biochemical equations are especially useful for determining whether the system of reactions goes in the forward or backward direction at specified T, P, pH, pMg, and I.
These recommendations apply also to reactions catalyzed by RNA enzymes (ref. 15), catalytic antibodies (ref. 16), and synthetic enzymes (ref. 17) (sometimes called ribozymes, abzymes, and synzymes, respectively). The reactions catalyzed have apparent equilibrium constants
In reporting results on equilibrium measurements on biochemical reactions it is extremely important to give enough information to specify T, P, pH, pMg (or free concentration of any other cation that is bound by reactants), and I at equilibrium. The most difficult of these variables are pMg and I. The calculation of pMg in principle requires information on the composition of the solution in terms of species, and this requires information on the dissociation constants of all of the weak acids and magnesium complex ions. However, if the metal ion binding constants of the buffer are known and the reactants are at low concentrations compared with the buffer, the concentrations of free metal ions can be calculated approximately. It is important to specify the composition of the solution and calculate the ionic strength, even if it can only be done approximately. Other important issues are the purities of materials, the methods of analysis, the question as to whether the same value of apparent equilibrium constant was obtained from both directions, and assignment of uncertainties. For calorimetric measurements, it is important to measure the extent of reaction. An important part of any thermodynamic investigation is the clear specification of the substances used and the reaction(s) studied. It is very helpful to readers to give Enzyme Nomenclature (ref. 13) identification numbers of enzymes and Chemical Abstracts Services registry numbers for reactants. IUPAC has published a "Guide to the Procedures for the Publication of Thermodynamic Data" (ref. 18), and CODATA has published a "Guide for the Presentation in the Primary Literature of Numerical Data Derived from Experiments" (ref. 19).
It is recommended that equilibrium and calorimetric measurements on biochemical reactions be carried out over as wide a range of temperature, pH, pMg, and I as is practical. For the study of biochemical reactions under "near physiological conditions," the following set of conditions is recommended: T = 310.15 K, pH = 7.0, pMg = 3.0, and I = 0.25 M. It is also recognized that there is no unique set of physiological conditions and that for many purposes it will be necessary and desirable to study biochemical reactions under different sets of conditions.
For the purpose of relating results obtained on biochemical reactions to the main body of thermodynamic data (NBS Tables and other tables listed in the Appendix) the results of experiments should be treated so as to yield results for a chemical (reference) reaction at T = 298.15 K and I = 0. If this calculation is done, the method of data reduction and all auxiliary data used should be reported. It is also recognized that while a standard state based upon the concentration scale has been widely used in biochemistry, the molality scale has significant advantages for many purposes and can also be used for the study of biochemical reactions and for the calculation of thermodynamic properties.
4. Alberty, R. A. (1992) Biophys. Chem. 42, 117-131.
5. Alberty, R. A. (1992) Biophys. Chem. 43, 239-254.
7. Alberty, R. A., and Goldberg, R. N. (1992) Biochemistry 31, 10610-10615.
9. Alberty, R. A. (1969) J. Biol. Chem. 244, 3290-3302.
10. Alberty, R. A. (1992) J. Phys. Chem. 96, 9614-9621.
11. Alberty, R. A., and Goldberg, R. N. (1993) Biophys. Chem. 47, 213-223.
12. Teague, W. E., and Dobson, G. P. (1992) J. Biol. Chem. 267, 14084-14093.
13. Webb, E. C. (1992) Enzyme Nomenclature, Academic Press, San Diego.
14. Alberty, R. A., and Cornish-Bowden, A. (1993) Trends Biochem. Sci. 18, 288-291.
15. Cech, T. R., Herschlag, D., Piccirilli, J. A., and Pyle, J. A. (1992) J. Biol. Chem. 256, 17479-82.
16. Blackburn, G. M., Kang, A. S., Kingsbury, G. A., and Burton, D. R. (1989) Biochem. J. 262, 381-391.
17. Pike, V. W. (1987) in Biotechnology (H.-J. Rehm and G. Reed, eds.), vol. 7a, 466-485, Verlag-Chemie.
18. "A Guide to the Procedures for the Publication of Thermodynamic Data", (1972) PureAppl. Chem. 289, 399-408. (Prepared by the IUPAC Commission on Thermodynamics and Thermochemistry.)
19. "Guide for the Presentation in the Primary Literature of Numerical Data Derived from Experiments". (February 1974) Prepared by a CODATA Task Group. Published in National Standard Reference Data System News.
Return to home page for Biochemical Thermodynamics.
i' are the apparent stoichiometric numbers of the reactants i in a biochemical reaction.
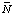 H(i )
H(i )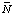 H(i )
H(i )riNH(i )
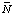 H(i )
H(i )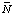 Mg(i )
Mg(i )![[Delta r]](../thgif/Deltar.gif) N (H+)
N (H+)![[Delta r]](../thgif/Deltar.gif) N (Mg2+)
N (Mg2+)![[Delta r]](../thgif/Deltar.gif) N (H+)
N (H+)![[Delta r]](../thgif/Deltar.gif) N (Mg2+)
N (Mg2+)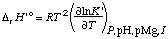 . . . . . . . . (32)
. . . . . . . . (32)![[Delta r]](../thgif/Deltar.gif) N (H+)
N (H+)![[Delta r]](../thgif/Deltar.gif) G 'o
G 'o![[Delta r]](../thgif/Deltar.gif) H 'o
H 'o![[Delta r]](../thgif/Deltar.gif) G '
G '![[Delta r]](../thgif/Deltar.gif) G ' =
G ' = ![[Delta r]](../thgif/Deltar.gif) G 'o + RT ln Q ' . . . . . . . . (34)
G 'o + RT ln Q ' . . . . . . . . (34)![[Delta r]](../thgif/Deltar.gif) G '
G '![[Delta r]](../thgif/Deltar.gif) H '
H '![[Delta r]](../thgif/Deltar.gif) S '
S '![[Delta r]](../thgif/Deltar.gif) G ' =
G ' = ![[Delta r]](../thgif/Deltar.gif) H ' - T
H ' - T![[Delta r]](../thgif/Deltar.gif) S ' . . . . . . . . (35)
S ' . . . . . . . . (35)![[Delta r]](../thgif/Deltar.gif) S ' =
S ' = ![[Delta r]](../thgif/Deltar.gif) S 'o - R ln Q ' . . . . . . . . (36)
S 'o - R ln Q ' . . . . . . . . (36)![[Delta r]](../thgif/Deltar.gif) H (cal)
H (cal)![[Delta r]](../thgif/Deltar.gif) H 'o
H 'o![[Delta r]](../thgif/Deltar.gif) H 'o =
H 'o = ![[Delta r]](../thgif/Deltar.gif) H(cal) -
H(cal) - ![[Delta r]](../thgif/Deltar.gif) N(H+)
N(H+)![[Delta r]](../thgif/Deltar.gif) Ho(HBuff) -
Ho(HBuff) - ![[Delta r]](../thgif/Deltar.gif) N(Mg2+)
N(Mg2+)![[Delta r]](../thgif/Deltar.gif) Ho(MgBuff) . . . . . . . . (38)
Ho(MgBuff) . . . . . . . . (38)![[Delta r]](../thgif/Deltar.gif) H o(HBuff) is the standard enthalpy for the acid dissociation of the buffer, and
H o(HBuff) is the standard enthalpy for the acid dissociation of the buffer, and ![[Delta r]](../thgif/Deltar.gif) H o(MgBuff)
H o(MgBuff)![[Delta r]](../thgif/Deltar.gif) N(H+)
N(H+)![[Delta r]](../thgif/Deltar.gif) N(Mg2+)
N(Mg2+)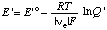 . . . . . . . . (39)
. . . . . . . . (39)![[Delta r]](../thgif/Deltar.gif) G 'o/|
G 'o/|e|F
![[Delta r]](../thgif/Deltar.gif) G 'o
G 'o![[Delta r]](../thgif/Deltar.gif) H 'o
H 'o![[Delta f]](../thgif/Deltaf.gif) G 'o
G 'o![[Delta f]](../thgif/Deltaf.gif) H 'o
H 'o![[Delta f]](../thgif/Deltaf.gif) S 'o
S 'o![[Delta r]](../thgif/Deltar.gif) G 'o =
G 'o =
i'
![[Delta f]](../thgif/Deltaf.gif) G 'o(i ) . . . . . . . . (40)
G 'o(i ) . . . . . . . . (40)i' are the apparent stoichiometric numbers of the reactants i in a biochemical reaction written in terms of reactants. These formation properties apply to reactants like ATP (that is, sums of species) at a specified T, P, pH, pMg, and I. The corresponding standard transformed entropy of formation of a reactant like ATP can be calculated using
![[Delta f]](../thgif/Deltaf.gif) G 'o(i ) =
G 'o(i ) = ![[Delta f]](../thgif/Deltaf.gif) H 'o(i ) - T
H 'o(i ) - T ![[Delta f]](../thgif/Deltaf.gif) S 'o(i ) . . . . . . . . (42)
S 'o(i ) . . . . . . . . (42)![[Delta f]](../thgif/Deltaf.gif) G o =
G o =![[Delta f]](../thgif/Deltaf.gif) H o
H o
![[Delta f]](../thgif/Deltaf.gif) H 'o/kJ mol-1
H 'o/kJ mol-1![[Delta f]](../thgif/Deltaf.gif) H 'o/kJ mol-1
H 'o/kJ mol-1ATP -2981.79 -2102.88 ADP -2000.19 -1231.48 AMP -1016.59 -360.38 A (adenosine) -5.34 529.96 Glc-6-P -2279.09 -1318.99 Glc (glucose) -1267.11 -426.70 CrP -1509.75 -750.37 Cr (creatine) -540.08 107.69 Pi -1299.13 -1059.55 H2O(l) -286.65 -155.66 ![[Delta r]](../thgif/Deltar.gif) G 'o
G 'o![[Delta r]](../thgif/Deltar.gif) G 'o
G 'o![[Delta r]](../thgif/Deltar.gif) G 'o,
G 'o, ![[Delta r]](../thgif/Deltar.gif) H 'o
H 'o![[Delta r]](../thgif/Deltar.gif) S 'o
S 'o![[Delta r]](../thgif/Deltar.gif) G 'o = (-1231.48 - 1318.99 + 2102.88 + 426.70) kJ mol-1
G 'o = (-1231.48 - 1318.99 + 2102.88 + 426.70) kJ mol-1![[Delta r]](../thgif/Deltar.gif) H 'o = (-2000.19 - 2279.09 + 2981.79 + 1267.11) kJ mol-1
H 'o = (-2000.19 - 2279.09 + 2981.79 + 1267.11) kJ mol-1![[Delta r]](../thgif/Deltar.gif) S 'o = (-30.38 + 20.89)x103 J mol-1/298.15 K = -31.83 J K-1 mol-1
S 'o = (-30.38 + 20.89)x103 J mol-1/298.15 K = -31.83 J K-1 mol-1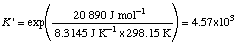
![[Delta r]](../thgif/Deltar.gif) G ',
G ', ![[Delta r]](../thgif/Deltar.gif) H ', and
H ', and ![[Delta r]](../thgif/Deltar.gif) S ' for the glucokinase reaction at 298.15 K, pH = 7, pMg = 3, and I = 0.25 M when the reactant concentrations are [ATP] = 10-5 M, [ADP] = 10-3 M, [Glc] = 10-4 M, and [Glc-6-P] = 10-2 M.
S ' for the glucokinase reaction at 298.15 K, pH = 7, pMg = 3, and I = 0.25 M when the reactant concentrations are [ATP] = 10-5 M, [ADP] = 10-3 M, [Glc] = 10-4 M, and [Glc-6-P] = 10-2 M.![[Delta r]](../thgif/Deltar.gif) G ' =
G ' = ![[Delta r]](../thgif/Deltar.gif) G 'o
G 'o![[Delta r]](../thgif/Deltar.gif) G ' is positive, the glucokinase reaction cannot occur in the forward direction under these conditions.
G ' is positive, the glucokinase reaction cannot occur in the forward direction under these conditions.![[Delta r]](../thgif/Deltar.gif) H ' =
H ' = ![[Delta r]](../thgif/Deltar.gif) H 'o
H 'o![[Delta r]](../thgif/Deltar.gif) S ' =
S ' = ![[Delta r]](../thgif/Deltar.gif) S 'o
S 'o![[Delta r]](../thgif/Deltar.gif) G ' =
G ' = ![[Delta r]](../thgif/Deltar.gif) H ' -
H ' - ![[Delta r]](../thgif/Deltar.gif) S '
S '![[Delta r]](../thgif/Deltar.gif) N(H+) = 0.62 at 298.15 K, 1 bar, pH = 7, pMg = 3, and I = 0.25 M. The convention is that H2O is omitted in the equilibrium expression for K or K ' when reactions in dilute aqueous solutions are considered.
N(H+) = 0.62 at 298.15 K, 1 bar, pH = 7, pMg = 3, and I = 0.25 M. The convention is that H2O is omitted in the equilibrium expression for K or K ' when reactions in dilute aqueous solutions are considered.pyruvate + carbonate + ATP = oxaloacetate + ADP + Pi . . . . . . . . (43)
C3H3O3- + HCO3- + ATP4- = C4H2O52- + ADP3- + HPO42- + H+ . . . . . . . . (44)
References for this section
Continue with 5 Thermodynamic Background.