 G o
G o H o
H o G o
G o H o
H o G 'o
G 'o H 'o
H 'o G 'o
G 'o H 'o
H 'o G o
G o H o
H o G 'o
G 'o H 'o
H 'o H 'o
H 'o H o
H o H 'o
H 'o H o
H o H 'o
H 'o H o
H o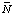 H(i )
H(i )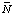 Mg(i )
Mg(i )
Contents of Section
6 Recommendations on Thermodynamic Tables
7 Nomenclature
8 References
9 Appendix: Survey of Current Biochemical Tables
The papers by Alberty (ref. 5) and Alberty and Goldberg (ref. 7) show four types of tables of thermodynamic properties of biochemical reactants: (1)  G o
G o H o
H o G o
G o H o
H o G 'o
G 'o H 'o
H 'o G 'o
G 'o H 'o
H 'o G o
G o H o
H o G 'o
G 'o H 'o
H 'o H 'o
H 'o H o
H o H 'o
H 'o H o
H o H 'o
H 'o H o
H o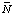 H(i )
H(i )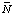 Mg(i )
Mg(i )
The choice of 298.15 K, 1 bar, pH = 7, pMg = 3, and I = 0.25 M is arbitrary, but these conditions are often used. Tables can be constructed for other conditions (T, pH, pMg, and I) if sufficient information is available. H2O has to be included in this table because its  G 'o(H2O)
G 'o(H2O) H 'o(H2O)
H 'o(H2O)
The most basic principle is that thermodynamic tables on biochemical reactants at pH = 7 and pMg = 3 should be consistent with the usual thermodynamic tables to as great an extent as possible. A great deal is already known about the thermodynamics of reactions in aqueous solution, and this is all of potential value in biochemistry. The standard transformed formation properties of inorganic phosphate and glucose 6-phosphate at pH = 7 and pMg = 3 can be calculated since the standard formation properties of inorganic phosphate and glucose are well known and the properties of glucose 6-phosphate can be calculated from  G 'o
G 'o H 'o
H 'o G o =
G o = H o
H o G 'o
G 'o H 'o
H 'o
For many biochemical reactants, the acid and magnesium complex dissociation constants have not been measured, but this does not mean that these reactants cannot be included in a table of  G 'o
G 'o H 'o
H 'o
The fact that biochemical reactions are often organized in series will facilitate the construction of thermodynamic tables. When a series starts or ends with a reactant with known formation properties, knowlege of the apparent equilibrium constants in the series makes it possible to calculate  G 'o
G 'o G 'o
G 'o G o
G o G o =
G o = H o
H o Gi 'o
Gi 'o
The following conventions are recommended:
1. When a reactant exists only in an electrically neutral form at pH = 7 and pMg = 3 and  G o
G o H o
H o G 'o
G 'o H 'o
H 'o
2. When a reactant exists in a single ionized form in the neighborhood of pH = 7 and pMg = 3, the values of  G o
G o H o
H o G 'o
G 'o H 'o
H 'o G 'o
G 'o G o
G o H o
H o
3. When a reactant exists in several ionized or complexed forms that are at equilibrium at pH = 7 and pMg = 3 and the standard thermodynamic properties of all of the ionized and complexed forms are known, the values of  G 'o
G 'o H 'o
H 'o
4. When a reactant exists in several ionized or complexed forms with known dissociation constants and  G o
G o H o
H o G 'o
G 'o H 'o
H 'o G o =
G o = H o
H o G o
G o H o
H o G 'o
G 'o H 'o
H 'o
5. If acid dissociation and magnesium dissociation constants are not known for a reactant, it can still be put into a table at pH = 7 and pMg = 3 if apparent equilibrium constants have been measured under these conditions for a reaction involving this reactant with other reactants whose transformed thermodynamic properties are known. Examples are the many reactants in glycolysis other than glucose, ATP, ADP, Pi, NAD, NADH, and H2O.
6. It is not necessary to have columns in tables for  S 'o
S 'o S o
S o
| Symbol | Name | Unit |
| A | extensive Helmholtz energy of a system | kJ |
| B | parameter in the extended Debye-Hückel theory | L-1/2 mol-1/2 |
| ci | concentration of species i | mol L-1 |
| co | standard state concentration (1 M) | mol L-1 |
 CPo CPo | standard heat capacity at constant pressure of reaction at T, P, and I | J K-1 mol-1 |
 CP'o CP'o | standard transformed heat capacity of reaction at constant T, P, pH, pMg, and I | J K-1 mol-1 |
| E | electromotive force | V |
| Eo | standard electromotive force of a cell or half cell | V |
| E ' | apparent electromotive force at specified pH | V |
| E 'o | standard apparent electromotive force of a cell or half cell at specified pH | V |
| F | Faraday constant (96 485.31 C mol-1) | C mol-1 |
| G | extensive Gibbs energy of a system | kJ |
| G ' | extensive transformed Gibbs energy of a system | kJ |
 G G | reaction Gibbs energy for specified concentrations of species at specified T, P, and I | kJ mol-1 |
 Go Go | standard reaction Gibbs energy of a specified reaction in terms of species at specified T, P, and I | kJ mol-1 |
 G ' G ' | transformed reaction Gibbs energy in terms of reactants (sums of species) for specified concentrations of reactants and products at specified T, P, pH, pMg, and I | kJ mol-1 |
 G 'o G 'o | standard transformed reaction Gibbs energy of a specified reaction in terms of reactants (sums of species) at specified T, P, pH, pMg and I | kJ mol-1 |
 G(i) G(i) | Gibbs energy of formation of species i at a specified concentration of i and specified T, P, and I | kJ mol-1 |
 Go(i) Go(i) | standard Gibbs energy of formation of species i at specified T, P, and I | kJ mol-1 |
 G '(i) G '(i) | transformed Gibbs energy of formation of species i or reactant i (sum of species) at specified concentration and specified T, P, pH, pMg, and I | kJ mol-1 |
 G 'o(i) G 'o(i) | standard transformed Gibbs energy of formation of species i or reactant i (sum of species) at specified T, P, pH, pMg, and I | kJ mol-1 |
| H | extensive enthalpy of a system | kJ |
| H ' | extensive transformed enthalpy of a system | kJ |
 H(cal) H(cal) | calorimetrically determined enthalpy of reaction that includes the enthalpies of reaction of H+ and Mg2+ (consumed or produced) with any buffer in solution | kJ mol-1 |
 H H | enthalpy of reaction of a specified reaction in terms of species at specified T, P, and I | kJ mol-1 |
 Ho Ho | standard enthalpy of reaction of a specified reaction in terms of species at specified T, P, and I | kJ mol-1 |
 H ' H ' | transformed enthalpy of reaction of a specified reaction in terms of reactants (sums of species) for specified concentrations of reactants and products at specified T, P, pH, pMg, and I | kJ mol-1 |
 H 'o H 'o | standard transformed enthalpy of a specified reaction in terms of reactants (sums of species) at specified T, P, pH, pMg and I | kJ mol-1 |
 H(i) H(i) | enthalpy of formation of species i at specified T, P, and I | kJ mol-1 |
 Ho(i) Ho(i) | standard enthalpy of formation of species i at specified T, P, and I | kJ mol-1 |
 H '(i) H '(i) | transformed enthalpy of formation of species i or reactant i (sum of species) at specified T, P, pH, pMg, and I | kJ mol-1 |
 H 'o(i) H 'o(i) | standard transformed enthalpy of formation of species i or reactant i (sum of species) at specified T, P, pH, pMg, and I | kJ mol-1 |
| I | ionic strength | mol L-1 |
| K | equilibrium constant for a specified reaction written in terms of concentrations of species at specified T, P, and I (omitting H2O when it is a reactant) | dimensionless |
| K ' | apparent equilibrium constant for a specified reaction written in terms of concentrations of reactants (sums of species) at specified T, P, pH, pMg, and I (omitting H2O when it is a reactant) | dimensionless |
| mi | molality of i | mol kg-1 |
| ni or n(i) | amount of species i | mol |
| n'(i) | amount of species (bound and unbound) or amount of reactant i (that is, sum of species) | mol |
| NH(i) | number of H atoms in species i | dimensionless |
| NMg(i) | number of Mg atoms in species i | dimensionless |
![[N bar]](../thgif/Nbar.gif) H(i) H(i) | average number of H atoms in reactant i at specified T, P, pH, pMg, and I | dimensionless |
 N(H+) N(H+) | change in binding of H+ in a biochemical reaction at specified T, P, pH, pMg, and I | dimensionless |
 N(Mg2+) N(Mg2+) | change in binding of Mg+2 in a biochemical reaction at specified T, P, pH, pMg, and I | dimensionless |
| NI | number of isomers in an isomer group | dimensionless |
| pH | -log10([H+]/c o) | dimensionless |
| pMg | -log10([Mg2+]/c o) | dimensionless |
| pX | -log10([X]/c o) | dimensionless |
| P | pressure | bar |
| Q | reaction quotient of specified concentrations of species in the same form as the equilibrium constant expression | dimensionless |
| Q ' | apparent reaction quotient of specified concentrations of reactants and products (sum of species) in the same form as the apparent equilibrium constant expression | dimensionless |
| R | gas constant (8.31451 J K-1 mol-1) | J K-1 mol-1 |
| ri or r(i) | equilibrium mole fraction of i within a specified class of molecules | dimensionless |
| S | extensive entropy of a system | J K-1 |
| S ' | extensive transformed entropy of a system | J K-1 |
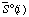 | standard molar entropy of species i at specified T, P, and I | J K-1 mol-1 |
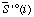 | standard molar transformed entropy of species i or reactant i at specified T, P, pH, pMg, and I | J K-1 mol-1 |
 S S | entropy of reaction of a specified reaction in terms of species at specified T, P, and I | J K-1 mol-1 |
 So So | standard entropy of reaction of a specified reaction in terms of ionic species at specified T, P, and I | J K-1 mol-1 |
 S ' S ' | transformed entropy of reaction of a specified reaction in terms of reactants (sums of species) for specified concentrations of reactants and products at specified T, P, pH, pMg, and I | J K-1 mol-1 |
 S 'o S 'o | standard transformed entropy of a specified reaction in terms of sums of species at specified T, P, pH, pMg and I | J K-1 mol-1 |
 So(i) So(i) | standard entropy of formation of species i at specified T, P, and I | J K-1 mol-1 |
 S 'o(i) S 'o(i) | standard transformed entropy of formation of species i or reactant i (sum of species) at specified T, P, pH, pMg, and I | J K-1 mol-1 |
| T | temperature | K |
| U | extensive internal energy of a system | kJ |
| V | volume | L |
| zi | charge of ion i with sign | dimensionless |
| density | kg m-3 | |
| chemical potential of species i at specified T, P, and I | kJ mol-1 | |
transformed chemical potential of species i or reactant (sum of species) at specified T, P, pH, pMg, and I [can be replaced by  G '(i )]i G '(i )]i | kJ mol-1 | |
standard chemical potential of species i at specified T, P, and I [can be replaced by  Go(i )] Go(i )] | kJ mol-1 | |
| number of electrons in a cell reaction | dimensionless | |
| stoichiometric number of species i in a specified chemical reaction | dimensionless | |
| apparent stoichiometric number of reactant i in a specified biochemical reaction | dimensionless |
1. Wadsö, I., Gutfreund, H., Privlov, P., Edsall, J. T., Jencks, W. P., Strong, G. T., and Biltonen, R. L. (1976) Recommendations for Measurement and Presentation of Biochemical Equilibrium Data, J. Biol. Chem. 251, 6879-6885; (1976) Q. Rev. Biophys. 9, 439-456.
2. Wadsö, I., and Biltonen, R. L.(1985) Recommendations for the Presentation of Thermodynamic Data and Related Data in Biology, Eur. J. Biochem. 153, 429-434.
3. Mills, I., Cvitas, T., Homann, K., Kallay, N., and Kuchitsu, K. (1988 and 1993) Quantities, Units and Symbols in Physical Chemistry, Blackwell Scientific Publications, Oxford.
4. Alberty, R. A. (1992) Biophys. Chem. 42, 117-131.
5. Alberty, R. A. (1992) Biophys. Chem. 43, 239-254.
6. Clarke, E. C. W., and D. N. Glew, D. N. (1966) Trans. Faraday Soc. 62, 539-547.
7. Alberty, R. A., and Goldberg, R. N. (1992) Biochemistry 31, 10610-10615.
8. Wilhoit, R. C. (1969) Thermodynamic Properties of Biochemical Substances, in Biochemical Microcalorimetry, H. D. Brown, ed., Academic Press, New York.
9. Alberty, R. A. (1969) J. Biol. Chem. 244, 3290-3302.
10. Alberty, R. A. (1992) J. Phys. Chem. 96, 9614-9621.
11. Alberty, R. A., and Goldberg, R. N. (1993) Biophys. Chem. 47, 213-223.
12. Teague, W. E., and Dobson, G. P. (1992) J. Biol. Chem. 267, 14084-14093.
13. Webb, E. C. (1992) Enzyme Nomenclature, Academic Press, San Diego.
14. Alberty, R. A., and Cornish-Bowden, A. (1993) Trends Biochem. Sci. 18, 288-291.
15. Cech, T. R., Herschlag, D., Piccirilli, J. A., and Pyle, J. A. (1992) J. Biol. Chem. 256, 17479-82.
16. Blackburn, G. M., Kang, A. S., Kingsbury, G. A., and Burton, D. R. (1989) Biochem. J. 262, 381-391.
17. Pike, V. W. (1987) in Biotechnology (H.-J. Rehm and G. Reed, eds.), vol. 7a, 466-485, Verlag-Chemie.
18. "A Guide to the Procedures for the Publication of Thermodynamic Data", (1972) PureAppl. Chem. 289, 399-408. (Prepared by the IUPAC Commission on Thermodynamics and Thermochemistry.)
19. "Guide for the Presentation in the Primary Literature of Numerical Data Derived from Experiments". (February 1974) Prepared by a CODATA Task Group. Published in National Standard Reference Data System News.
20. Alberty, R. A., and Oppenheim, I. (1988) J. Chem. Phys. 89, 3689-3693.
21. Alberty, R. A., and Oppenheim, I. (1992) J. Chem. Phys. 96, 9050-9054.
22. Wyman, J., and Gill, S. J. (1990) Binding and Linkage, University Science Books, Mill Valley, CA.
23. Smith, W. R., and Missen, R. W. (1982) Chemical Reaction Equilibrium Analysis: Theory and Algorithms, Wiley-Interscience, New York.
24. Alberty, R. A. (1983) I & EC Fund. 22, 318-321.
25. Goldberg, R. N., and Tewari, Y. B. (1989) J. Phys. Chem. Ref. Data 18, 809-880.
26. Larson, J. W., Tewari, Y. B., and Goldberg, R. N. (1993) J. Chem. Thermodyn. 25, 73-90.
27. Goldberg, R. N., and Tewari, Y. B. (1991) Biophys. Chem. 40, 241-261.
28. Clarke, E. C. W., and Glew, D. N. (1980) J. Chem. Soc., Faraday Trans. 1 76, 1911-1916.
29. Pitzer, K. S. (1991) Ion Interaction Approach: Theory and Data Correlation, in Activity Coefficients in Electrolyte Solutions, 2nd Edition, K. S. Pitzer, editor, CRC Press, Boca Raton, Fla.
30. Record, M. T., Anderson, C. F., and Lohman, T. M. (1978) Q. Rev. Biophys. 11, 2.
31. Anderson, C. F., and Record, M. T. (1993) J. Phys. Chem. 97, 7116-7126.
32. Alberty, R. A. (1993) Pure Appl. Chem. 65, 883-888.
33. Guynn, R. W., and Veech, R. L. (1973) J. Biol. Chem. 248, 6966-6972.
34. Alberty, R. A. (1991) J. Chem. Educ. 68, 984.
35. Alberty, R. A. (1992) J. Chem. Educ. 69, 493.
36. Alberty, R. A. (1994) Biophys. Chem. 49, 251-261.
9. APPENDIX: SURVEY OF CURRENT BIOCHEMICAL THERMODYNAMIC TABLES
(The reader is cautioned on distinguishing chemical reactions from biochemical reactions.)
1. Burton, K., Appendix in Krebs, H. A., and Kornberg, H. L. (1957) Energy Transformations in Living Matter, Springer-Verlag, Berlin.
2. Atkinson, M. R., and R. K. Morton, R. K. (1960) in Comparative Biochemistry, Volume II, Free Energy and Biological Function, Florkin, M., and Mason, H. (eds.), Academic Press, New York.
3. Wilhoit, R. C. (1969) Thermodynamic Properties of Biochemical Substances, in Biochemical Microcalorimetry, H. D. Brown (ed.), Academic Press, New York. This article gives standard thermodynamic properties of a large number of species at zero ionic strength. In a separate table standard enthalpies and standard Gibbs energies of formation of adenosine phosphate species are given relative to H2ADP- at 298.15 K.
4. Thauer, R. K., Jungermann, K., and Decker, K. (1977) Bacteriological Reviews 41, 100-179. Standard Gibbs energies of formation of many species of biochemical interest at 298.15 K. Table of standard Gibbs energies of reaction corrected to pH 7 by adding  G o(H+)
G o(H+)
5. Goldberg, R. N. (1984) Compiled thermodynamic data sources for aqueous and biochemical systems: An annotated bibliography (1930-1983), National Bureau of Standards Special Publication 685, U. S. Government Printing Office, Washington, D. C. A general and relatively complete guide to compilations of thermodynamic data on biochemical and aqueous systems.
6. Rekharsky, M. V., Galchenko, G. L., Egorov, A. M., and Berezin, I. V. (1986) Thermodynamics of Enzymatic Reactions, in Thermodynamic Data for Biochemistry and Biotechnology, H.-J. Hinz (ed.), Springer-Verlag, Berlin. Tables of  H o
H o G o
G o S o
S o
7. Goldberg, R. N., and Tewari, Y. B. (1989) Thermodynamic and Transport Properties of Carbohydrates and their Monophosphates: The Pentoses and Hexoses, J. Phys. Chem. Ref. Data 18, 809-880 . Values on a very large number of reactions at 298.15 K carefully extrapolated to zero ionic strength.  H o
H o G o
G o
8. Miller, S. L., and Smith-Magowan, D. (1990) The Thermodynamics of the Krebs Cycle and Related Compounds, J. Phys. Chem. Ref. Data 19, 1049-1073. A critical evaluation for a large number of reactions and properties of substances at 298.15 K.
9. Goldberg, R. N., and Tewari, Y. B. (1991) Thermodynamics of the Disproportionation of adenosine 5'-diphosphate to adenosine 5'-triphosphate and Adenosine 5'-monophosphate, Biophys. Chem. 40, 241-261. Very complete survey of data on this reaction and on the acid dissociation and magnesium complex dissociations involved.
10. Goldberg, R. N., Tewari, Y. B., Bell, D., Fazio, K., and Anderson, E. (1993) Thermodynamics of Enzyme-Catalyzed Reactions; Part 1. Oxidoreductases, J. Phys. Chem. Ref. Data, 22, 515-582. This review contains tables of apparent equilibrium constants and standard transformed molar enthalpies for the biochemical reactions catalyzed by the oxidoreductases.
11. Goldberg, R. N., and Tewari, Y. B. (1994) Thermodynamics of Enzyme-Catalyzed Reactions: Part 2. Transferases, J. Phys. Chem. Ref. Data 23, 547-617.
Standard Thermodynamic Tables
1. Wagman, D. D., Evans, W. H., Parker, V. B., Schumm, R. H., Halow, I., Bailey, S. M., Churney, K. L., and Nutall, R. L. (1982) The NBS Tables of Chemical Thermodynamic Properties, J. Phys. Chem. Ref. Data, 11, Suppl. 2.
2. Cox, J. D., Wagman, D. D., and Medvedev, M. V. (1989) CODATA Key Values for Thermodynamics, Hemisphere, Washington, D. C.