E + Z
Recommendations on the symbols and terminology of enzyme kinetics were previously made in conjunction with the recommendations of the Commission on Biochemical Nomenclature and Classification of Enzymes, and were published in Enzyme Nomenclature (1972) [1] and in earlier editions. During preparation of Enzyme Nomenclature (1978) [2] by NC-IUB it was agreed that the symbols and terminology of enzyme kinetics were properly distinct from the nomenclature of enzymes and should therefore be omitted from a compilation of enzyme names. In consequence the 1972 recommendations [1] have remained in operation even though they take little account of the developments of the subject in the past two decades, particularly the increased interest in reactions with two or more substrates. Accordingly, during 1978-1979 the views of numerous biochemists active in enzyme kinetics were solicited by NC-IUB and subsequently a panel was set up to make new recommendations.
To minimize differences between chemical and biochemical practice, the Report on Symbolism and Terminology in Chemical Kinetics [3] produced by IUPAC in 1980 has been followed where appropriate. Such differences as remain are the consequence of long-standing biochemical practice or of the fact that enzyme-catalysed reactions usually have simple overall stoichiometries and take place at constant pressure in the liquid phase and so require little attention to some details that may be crucial in chemical kinetics.
Certain conflicts that have greatly exercised some biochemists now seem less important than they may have done in the past. For example, because of the great diversity of enzyme mechanisms it is unlikely that any one system of numbering rate constants can satisfy all possible needs. It is much more important that rate constants be clearly defined in the context in which they are used than that they should satisfy any universal system Thus although this report follows the IUPAC recommendations [3,4] in its examples for illustration it is not implied that these should be used without definition or in all circumstances.
We have adopted the general policy of taking an operational approach to definitions, terms and symbols, rather than basing them on assumed mechanisms. In other words, definitions refer to what one observes, not to the way it is interpreted. This seems to be the safest course in kinetics, and particularly in enzyme kinetics, as conclusions about mechanisms often have to be revised in the light of further investigations, whereas the observations, if they are properly carried out, do not. Definitions based on what is actually observed are therefore on a sounder and more lasting basis than those that depend on an assumed mechanism. In Section 11 we do, however, consider mechanisms briefly.
A catalyst is a substance that increases the rate of a reaction without modifying the overall standard Gibbs-energy change in the reaction. This definition is equivalent to the statement that the catalyst does not appear in the stoichiometric expression of the complete reaction. Catalysts are said to exert a catalytic action, and a reaction in which a catalyst is involved is called a catalysed reaction.
Kinetic equations are commonly expressed in terms of the amount-of-substance concentrations of the chemical species involved The amount-of-substance concentration is the amount of substance (for which the SI unit is the mole, symbol mol) divided by the volume. As it is the only kind of concentration commonly used in biochemistry it is usually abbreviated to concentration and this shorter form will be used in the remainder of this document without further discussion. The unit almost invariably used for concentration is mol dm-3, which is alternatively written as to mol L-1, mol l-1, or simplyÊMÊ(molar).
An enzyme is a protein that acts as a catalyst.
A substrate is a reactant (other than a catalyst) in a catalysed reaction.
An inhibitor is a substance that diminishes the rate of a chemical reaction and the process is called inhibition. In enzyme-catalysed reactions an inhibitor frequently acts by binding to the enzyme, in which case it may be called an enzyme inhibitor. An activator is a substance, other than the catalyst or one of the substrates, that increases the rate of a catalysed reaction. An activator of an enzyme-catalysed reaction may he called an enzyme activator if it acts by binding to the enzyme.
The terms effector and modifier are general terms that apply to substances that interact with enzymes and either increase or decrease their catalytic action. Enzyme inhibitors and enzyme activators are therefore special cases of effectors and modifiers. The term effector is more commonly used when the substance produces effects of physiological significance, whereas the term modifier is more appropriate for a substance that is artificially added to an enzyme system being studied in vitro.
Sometimes added substances increase or decrease the rate of an enzyme-catalysed reaction without interacting with the enzyme itself; they may interact with substrates or with modifiers or effectors that are already present in the system. Such substances may be referred to as activators or inhibitors, but should not be referred to as enzyme activators, enzyme inhibitors, modifiers or effectors.
A typical overall enzyme-catalysed reaction involving a single substrate and.a single product may be written as
E + Z where E is the enzyme, A the substrate and Z the product. The double arrows indicate that the reaction occurs in both directions. When two or more substrates and two or more products are involved, the overall reaction may be written as
E + Z + Y + . . . It is convenient to use early letters of the alphabet for substrates and late letters for products. However, the letter S is frequently used for the substrate of a one-substrate reaction, and P, Q, R are often used for products. In general, any consistent system may be used and the symbols should always be defined. Although the enzyme E is included for completeness in these two examples, it is usually omitted because it is not necessary for specifying the overall stoichiometry of a reaction.
Many of the terms defined in this document, especially in this section, such as catalyst, substrate, order of reaction, steady state, etc., are not unique to enzyme kinetics, but have a wide currency in chemistry. The definitions given here are not intended to conflict with those recommended for use by chemists [5], but because of the special needs of enzyme kinetics they are not necessarily identical.
2.1. Rates of Consumption and Formation
The rate of consumption of a reactant of concentration [A] is defined as
. . . . . . . . (1)
in which t represents time. Square brackets may be used without definition to indicate concentrations, e.g. [A] is the concentration of A. Other symbols, such as a for the concentration of A, may be used for typographical convenience, but these should be defined. The rate of formation of a substance of concentration [Z] is defined as
. . . . . . . . (2)
The usual unit of rate is mol dm-3 s-1 or mol L-1 s-1 (where L = liter 
dm3) or M s-1 (where M, molarity, = mol dm-3). In all contexts the term velocity may be used as a synonym for rate. The alternative will only be mentioned in these Recommendations, however, when it appears to be the more common usage.
In a given reaction the rates of consumption and rates of formation are equal to one another only if there is a one-to-one stoichiometric relationship between the species consumed and formed. For example, in a reaction with stoichiometry
2Z the rate of formation of Z is twice the rate of consumption of A, and the rate of consumption of B is three times that of A. In most enzyme-catalysed reactions, however, there is a one-to-one stoichiometric ratio between all substrates and products. It is then permissible to omit the subscript from v and use the term rate of reaction.
For a reaction of stoichiometry
E + Z at a given time the rate of formation of Z is equal to the rate of consumption of A, and can be called the rate of reaction, v:
. . . . . . . . (3)
A similar set of relationships applies when there are several reactants in one-to-one stoichiometry. Complications arise if a one-to-one stoichiometry between all substrates and all products does not exist. This can arise in two ways:
a) The overall stoichiometry may be, for example,
2Z. The numbers -1, -3 and 2 are the stoichiometric coefficients of A, B and Z respectively in this reaction; by convention they are positive for products and negative for reactants. For a reaction of this kind the rate of reaction is the rate of consumption or formation of any reactant divided by the appropriate stoichiometric coefficient, i.e. (in this example):
. . . . . . . . (4)
This situation rarely arises in enzyme kinetics.
b) Intermediates may be formed in amounts comparable with those of reactants, for example
L E + Z + Y. This gives rise to time-dependent stoichiometry and there is not a one-to-one relationship between the amounts of reactants. It is not then permissible to speak of rate of reaction for the complete reaction, though it may be meaningful to define rates of reaction for the individual steps. Time-dependent stoichiometry occurs in the pre-steady-state phase of enzyme-catalysed reactions (Section 9), during which the amount of intermediate formed is comparable with the amounts of product.
The rate of reaction as defined here is an intensive quantity with dimensions of concentration divided by time. It conforms with almost universal usage in kinetics and with the current (1980) recommendations of IUPAC [3], but differs from earlier IUPAC recommendations, in which the term rate of reaction referred to the corresponding extensive quantity with dimensions of amount of substance divided by time. There is little evidence that this latter recommendation has ever been widely adopted and in the context of enzyme kinetics it is recommended that the term rate of reaction be used exclusively for the intensive quantity as defined above. If the extensive quantity is required it may be termed the rate of conversion and symbolized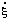 
[3, 5].
Note An intensive quantity is one like temperature or density that does not depend on the amount of material being considered and may be contrasted with an extensive quantity, such as heat or mass which does. (See also Addendum 1.)
2.3. Elementary and Composite Reactions
An elementary reaction is one in which no reaction intermediates have been detected or need be postulated to describe the chemical reaction on a molecular scale. Such reactions are said to occur in a single step.
The term molecularity, which applies only to an elementary reaction, refers to the number of molecular particles involved in the microscopic chemical event. With reactions in solution, solvent molecules are counted in the molecularity if they enter into the overall process, but not if they merely exert an environmental or solvent effect. For example. the formation of an enzyme-substrate complex in aqueous solution.
EA has a molecularity of two and is said to be bimolecular. The reverse process in solution,
E + A has a molecularity of unity and is said to be unimolecular. The hydrolysis of an acyl-enzyme, in which water enters into the process,
E-H + R-COOH is bimolecular.
Virtually all enzyme-catalysed overall reactions occur in more than one elementary step and are described as composite reactions. The terms complex reaction may also be used with the same meaning. Simple examples in enzyme kinetics are as follows:
EA EZ E + Z
E + A + B EA + B EAB EYZ EY + Z E + Y + Z
3. ORDER OF REACTION, AND RATE CONSTANT
The term order of reaction can be applied to any elementary reaction considered in one direction only, and to certain composite reactions.
For an elementary reaction occurring in one direction the order of reaction is equal to the molecularity, but it describes the kinetics not the mechanism. Thus, for the unimolecular elementary process
E + Athe rate of reaction is proportional to the concentration of the reactant EA:
v = k [EA] . . . . . . . . (5)
As the concentration [EA] is raised to the first power the order is unity and the reaction is said to be first order. The constant k is known as the rate constant of the reaction.
For the bimolecular elementary process
EA the rate is proportional to the product of the reactant concentrations:
v = k [E] [A] . . . . . . . . (6)
The reaction is first-order in E, first-order in A, but second-order overall, and k is again the rate constant. The orders for the individual reactants, unity for E and unity for A, are known as partial orders and the sum of all the partial orders of a reaction is the overall order.
Second-order rate constants, such as k in Eqn (6), have the dimensions of reciprocal concentration multiplied by reciprocal time, whereas first-order rate constants, such as k in Eqn (5), have the dimensions of reciprocal time. This difference in dimensions is not normally evident from the symbols used to represent rate constants, and care must therefore be taken to avoid making improper comparisons between rate constants of different orders. It is sometimes convenient to multiply a second-order rate constant by an appropriate concentration to produce a quantity with the dimensions of a first-order rate constant, e.g. k [A] from Eqn (6); such a product is called a pseudo-first-order rate constant. The units of rate constants vary with the order of reaction in the same way that their dimensions vary. For a first-order rate constant, such as k in Eqn (5), the units are s-1 . For a second-order rate constant, such as k in Eqn (6), the units are dm3 mol-1 s-1 or L mol-1 s-1 or M-1 s-1.
The concept of order of reaction (but not molecularity) can also be applied to certain reactions that occur by composite mechanisms, provided that the rate is proportional to reactant concentrations raised to powers (which need not be integral). However, this is rarely the case with enzyme-catalysed reactions and the concept of order cannot therefore be applied strictly to such reactions overall. Nonetheless the individual steps of composite reactions have orders when considered in one direction. For processes that do not have a true order it is sometimes convenient to define an apparent order with respect to a reactant A as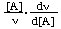 
(or as 
, which is equivalent). For many enzyme-catalysed reactions the true order with respect to any substrate approximates to unity at very low concentrations and to zero at very high concentrations, but is not defined at intermediate concentrations. The apparent order, on the other hand, exists at any concentration.
It is sometimes useful to consider the rates of unidirectional elementary steps of a composite reaction in isolation. When the use of the term rate of reaction for such rates would cause ambiguity the term chemical flux or chemiflux may be used instead. For a full discussion of this terminology, see the IUPAC recommendations [3]. In enzyme kinetics the need for an unambiguous terminology occurs mainly in discussions of the use of rates of transfer of isotopic labels as probes of the chemical fluxes in different parts of the composite reaction.
The elementary reactions in a composite mechanism should be numbered as systematically as possible and in such a way that reverse processes are easily recognized. The reaction numbers should be used as subscripts to k, for rate constants, or v, for the individual rates (chemical fluxes). The preferred scheme for ordinary use is:
1) k1, k-1, k2, k-2 . . . . ; v1, v-1, v2, v-2, . . .
In this scheme positive subscripts may be prefixed by a + sign, i.e. k1 may be written as k+1, if it helps avoid ambiguity resulting from confusion with scheme 3 (below), or to emphasize that it refers to a step in the forward direction of the reaction. For some kinds of computer application and for theoretical discussions of enzyme mechanisms it is sometimes convenient to number the different forms of the enzyme rather than the elementary steps and then to denote the step from (e.g.) E3 to E4 as 34, etc. With this scheme the numbering of enzyme forms must be given explicity and the rate constants and rates listed above might become
2) k12, k21, k23, k32, . . .; v12, v21, v23, v32, . . .
If there are more than nine enzyme forms in the mechanism the subscripts should be separated by a comma, e.g. k10,11 but this can be omitted when it is not required for clarity.
The following scheme, in which odd subscripts refer to forward steps and even subscripts to reverse steps:
3) k1, k2, k3, k4 . . . . ; v1, v2, v3, v4, . . .
is less satisfactory, both because it conflicts with IUPAC Recommendations [3] and because it makes it more difficult to recognize the forward and reverse rate constants for particular steps.
It is unrealistic to expect any universal system of numbering rate constants to be equally satisfactory in all circumstances. For example, in a mechanism where enzyme forms in different states of protonation can undergo analogous reactions it may be clearer to assign the same numbers to the analogous steps and distinguish between them by the use of primes, etc., rather than try to apply any of the above schemes in a rigid way. Regardless of what system is used, rate constants should never be referred to except in explicit relation to a mechanism or to a kinetic equation.
3.2. Steady-State Approximation
If an intermediate is always present in amounts much less than those of the reactants (other than the enzyme) the rate of change of its concentration is much smaller than that of the reactants. This condition is ensured whenever, as is usually the case in enzyme-catalysed reactions, the concentration of substrate is much higher than that of the enzyme; it is not necessary for the amount of intermediate to be small compared with the amount of enzyme. For example, in the scheme
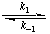EA 
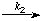E + Z if [EA] is always much less than [A] the following equation is obeyed to a good approximation:
. . . . . . . . (7)
The intermediate EA is said to be in a steady state. The use of this approximation to obtain an overall rate expression is known as the steady-state treatment or the steady-state approximation.
At the very beginning of the reaction the concentration of EA in the above scheme is rising from zero to its steady-state value. The steady-state approximation is not valid during these early times and the kinetics are known as pre-steady-state kinetics or transient-phase kinetics. The transient phase of an enzyme-catalysed reaction usually occupies a very brief period of time (usually a small fraction of a second), and special techniques must be used for investigating this phase of the reaction (Section 9).
The rate of reaction of an enzyme-catalysed reaction is not defined during the transient phase, because there is not a one-to-one stoichiometry between the reactants (see section 2.2). In the steady state a one-to-one stoichiometry is established and the rate of reaction can be defined. This rate, extrapolated back to zero time, is called the initial rate and given the symbol v0. The subscript 0 is normally omitted when no other kinds of rate are at issue, i.e. when extended time courses are not being analysed.
The ratio [E] [A]/[EA] at equilibrium is called the substrate dissociation constant and given the symbol KsA When only one substrate is in question the qualifier A may be omitted, and when it is included its location is a matter of typographical convenience. The substrate dissociation constant should not be confused with the Michaelis constant KmA (see section 4.1, below), to which it bears no necessary relationship in general. In the example given above KsA is equal to the ratio k-1/k1.
1. International Union of Pure and Applied Chemistry and International Union of Biochemistry (1973) Enzyme Nomenclature, Recommendations 1972, Elsevier, Amsterdam.
2. Nomenclature Committee of the International Union of Biochemistry (1979) Enzyme Nomenclature, Recommendations 1978, Academic Press, New York.
3. International Union of Pure and Applied Chemistry (1981) Symbolism and terminology in chemical kinetics, 1980, Pure Appl. Chem. 53, 753 - 771.
4. International Union of Pure and Applied Chemistry (1979) Manual of Symbols and Terminology for Physicochemical Quantities and Units, Pergamon Press, Oxford; also in Pure Appl. Chem. 51, 1-41 (1979).
5. International Union of Pure and Applied Chemistry (1979) Glossary of terms used in physical organic chemistry (Gold, V., ed.) Pure Appl. Chem. 51, 1725-1801. [revised edition Pure Appl. Chem. 1994, 66, 1077-1184]
Return to home page for Enzyme Kinetics.