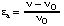. . . . . . . . (23)
Contents of Section
An activator is a substance, other than the catalyst itself or one of the substrates, that increases the rate of an enzyme-catalysed reaction, and it is said to bring about activation. If a reaction in the absence of an activator occurs with rate vo, the degree of activation is given by
This equation is analogous to the definition of degree of inhihition (Eqn 20) and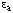 
is, like 
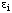, dimensionless. In general, the equations for activation closely resemble those for inhibition: wherever a term of the form (1 + [I]/Ki) appears in an inhibition equation, a corresponding term with (I + K/[Q]) can be written for activation of the same kind by an activator Q.
Activation has been studied much less than inhibition. and at present no system of terminology enjoys wide currency. Nonetheless, the rather unsatisfactory term competitive activation is occasionally used (see below), and the following classification is offered in the hope of providing a more appropriate terminology. The fundamental division is between linear activation which can be fully defined by terms in the denominator of the rate expression that are linear in the reciprocal concentration of activator, i.e. terms of the form (1 + K/[Q]), and non-linear activation. which cannot. An alternative division is between essential activation. in which the rate is zero in the absence of activator, and non-essential activation, in which it is finite. These two classifications overlap to a large extent but are not identical: linear activation must be essential. and non-essential activation must be non-linear, but essential activation can in principle be non-linear. Linear activation can, like linear inhibition, be usefully classified further according to whether the activation affects the apparent value of the specificity constant, in which case it is called specific activation, the apparent value of the catalytic constant, in which case it is called catalytic activation, the apparent value of the Michaelis constant, in which case it is called binding activation, or some combination of these, in which case it is called mixed activation. There is no sense in which specific activation can be regarded as resulting from competition between activator and substrate; consequently the term competitive activation is meaningless and to be avoided: the terms uncompetitive and non-competitive are also best avoided in the context of activation.
The rates of enzyme-catalysed reactions vary with pH and often pass through a maximum as the pH is varied. If the enzyme obeys Michaelis-Menten kinetics the kinetic parameters k0 and kA often behave similarly. The pH at which the rate or a suitable parameter is a maximum is called the pH optimum and the plot of rate or parameter against pH is called a pH profile. Neither the pH optimum nor the pH profile of an enzyme has any absolute significance and both may vary according to which parameter is plotted and according to the conditions of the measurements.
If the pH is changed and then brought back to its original value, the behaviour is said to be reversible if the original properties of the enzyme are restored; otherwise it is irreversible. Reversible pH behaviour may occur over a narrow range of pH, but effects of large changes in pH are in most cases irreversible.
The diminution in rate as the pH is taken to the acid side of the optimum can be regarded as inhibition by hydrogen ions. The diminution in rate on the alkaline side can be regarded as inhibition by hydroxide ions. The equations describing pH effects are therefore analogous to inhibition equations. For single-substrate reactions the pH behaviour of the parameters k0 and kA can sometimes be represented by an equation of the form
. . . . . . . . (24)
in which k represents k0 or kA, and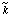 
is the value of the same parameter that would be observed if the enzyme existed entirely in the optimal state of protonation; it may be called the pH-independent value of the parameter. The constants K1 and K2 can sometimes be identified as acid dissociation constants for the enzyme. substrates or other species in the reaction mixture. The identification is, however, never straight forward and has to be justified by independent evidence. The behaviour is frequently much more complicated than represented by Eqn (24).
It is not accidental that this section has referred exclusively to pH dependences of k0 and kA. The pH dependence of the initial rate or, worse, the extent of reaction after a given time is rarely meaningful; the pH dependence of the Michaelis constant is often too complex to be readily interpretable.
9. PRE-STEADY-STATE KINETICS
The pre-steady-state or transient phase in enzyme-catalysed reactions occupies very short periods (usually fractions of a second) and very low product concentrations. Special techniques therefore have to be used. For reactions that are not too fast the stopped-flow technique, in which the enzyme and reactants are rapidly mixed and the flow stopped. is commonly used.
For reactions that have to be studied over periods of less than 1 ms relaxation techniques are used. In these techniques the system is disturbed, usually but not necessarily from a state of equilibrium, after which it relaxes to equilibrium or a new steady state. In the temperature-jump (T jump) technique the temperature is increased rapidly and the system relaxes to a new state of equilibrium or a new steady state at the final temperature. In the pressure-jump technique the pressure is rapidly changed.
The relaxation time
10. NON-MICHAELIS-MENTEN KINETICS
Some enzymes display non-Michaelis-Menten kinetics that do not approximate to Michaelis-Menten kinetics to any useful extent. In such case there is little value in retaining the terminology and symbolism of Michaelis-Menten kinetics. Instead it is often possible to express the rate as a rational function of the substrate concentration:
(In principle this kind of equation can be generalized to accommodate more than a single substrate but it then becomes highly complicated and only the single-substrate case will be considered here.) A rational function is a ratio of two polynomials. The degree of a polynomial is the largest exponent: thus, the degree of the numerator of the expression in Eqn (25) is n and that of the denominator is m. The rational function as a whole may be described as a 'n:m function'. In general the degree of the numerator of a rate equation does not exceed the degree of the denominator for enzyme-catalysed reactions, but there is no other necessary relationship between n and m and neither bears any necessary relationship to the number of catalytic centres per molecule of enzyme. In the terminology of Eqn (25) any rate equation obeying Michaelis-Menten kinetics can be defined as a 1:1 function.
Any coefficient
Under some conditions, which cannot be expressed simply and are not normally obvious from inspection of the coefficients of Eqn (25), the equation may generate a plot of v against [A] that shows a monotonic increase in v towards a limiting value at all positive finite values of [A]. A necessary, but not sufficient, condition is that the degrees of the numerator and denominator be equal, i.e. n = m. It is then meaningful to define a limiting rate V =
The term co-operativity is sometimes restricted to a purely mechanistic meaning, i.e. it is considered to refer to interactions between distinct sites on the enzyme. In common practice, however, the terms discussed above are frequently applied to enzymes in the absence of clear evidence for such interactions, and the aim therefore has been to legitimize such usage by providing purely operational definitions. In contexts where it is considered necessary to emphasize the operational character of the kind of co-operativity defined in terms of the Hill coefficient it may be qualified as Hill co-operativity or kinetic co-operativity.
11. TYPES OF MECHANISM FOR ENZYMIC CATALYSIS
The definitions given so far have been operational, i.e. they provide a way of describing what may be observed independently of any interpretation that may been placed on it. Little has been said about mechanisms, i.e., the detailed descriptions of the chemical events that make up the catalytic process. Nonetheless, the ultimate objective of most investigations in enzyme kinetics is to propose a mechanism. It is to be emphasized at the outset that a kinetic investigation can disprove a proposed mechanism but can never establish a mechanism beyond doubt. A mechanism may be consistent with all of the known facts, yet it is always possible to propose other mechanisms that are also consistent with the facts.
The procedure that is adopted, and the only one that allows progress to be made, is to accept the simplest mechanism that is consistent with all the known facts. This is the principle of Occam's razor. A steady-state study of the effect of substrate concentrations on the rate, leading to an empirical rate equation, can often lead to a proposed mechanism. Such a mechanism can be tested by additional investigations, such as of the pre-steady-state kinetics, and of the effects of inhibitors, pH, temperature and solvent composition.
It is not a practical proposition to institute a consistent system for naming mechanisms, although attempts to do this have been made, because except in the most trivial cases it is always simpler and clearer to specify a mechanism by reference to a scheme. Nonetheless, certain terms occur frequently in the descriptions of mechanisms of enzymic catalysts and will be defined here.
The form of an enzyme that exists in solution in the absence of any substrate or other small molecule that can bind to it is called the free enzyme. An intermediate derived from the free enzyme by binding of a substrate molecule is called an enzyme-substrate complex, and terms such as enzyme-product complex, enzyme-inhibitor complex, EA complex may also be used by an obvious extension of this definition. A complex derived from the free enzyme and one other molecule is called a binary complex; one derived from the free enzyme and two other molecules is called a ternary complex; one derived from the free enzyme and three other molecules is called a quaternary complex. If the catalytic process proceeds through a second form of free enzyme that differs from the first by the presence of a covalently bound group that is transferred in the reaction this second form of free enzyme is called a substituted enzyme.
Complexes that do not undergo further reactions that are part of the catalytic pathway are called dead-end complexes, and the reactions producing them are called dead-end reactions. Enzyme-substrate complexes that do not lead to reaction, which are often but not necessarily dead-end complexes, are called abortive or non-productive complexes.
When a reaction proceeds through a series of steps that must occur in a specified order, e.g. the substrates must bind in a particular order and the products are released in a particular order, it is said to obey a compulsory-order mechanism. (The alternative term linear mechanism is sometimes used, but it is discouraged because it can invite confusion with other uses of the term linear in enzyme kinetics.) When this is not the case the reaction is said to follow a random-order mechanism or a branched mechanism. These terms may also be applied to parts of mechanisms: for example, it may happen that substrates bind in random order but products are released in a compulsory order. The distinction between compulsory-order and random-order mechanisms is rarely absolute in practice. The term preferred-order mechanism may be used to emphasize that although more than one pathway exists most of the flux is through one of them. The term random-order mechanism does not, however, exclude this intermediate case unless explicitly stated to do so.
Elementary steps in which the enzyme forms complexes with small molecules are called binding steps and the reverse steps are called release steps, usually with a qualifier to indicate the type of species bound or released: e.g. substrate binding step or product-release step, etc. Elementary steps in which no binding or release occurs may be called isomerizations.
An allosteric effector is one that acts by binding to the enzyme at a site different from the active site. There is no necessary connection between allosteric effects and co-operative effects, though they often occur together in real systems.
The catalytic activity of an enzyme is the property measured by the increase in the rate of conversion (i.e. the rate of reaction multiplied by the volume: see Section 2.2) of a specified chemical reaction that the enzyme produces in a specified assay system [6]. This is an extensive quantity, and quantities derived from it include specific catalytic activity (used for following enzyme purification), which is the catalytic activity divided by the mass of protein, and molar catalytic activity, which is the catalytic activity divided by the amount of substance, either of enzyme catalytic centres or of multi-centre molecules. In the latter case it is important to specify whether the measurements refer to catalytic centres or to molecules. Molar catalytic activity has the dimensions of reciprocal time, like first-order rate constants; if it refers to catalytic centres it will approach k0, the catalytic constant (Section 4.1), if the conditions in the assay are such that v approaches V.
13. SUMMARY OF RECOMMENDED SYMBOLS AND UNITS
Table 1 lists the symbols recommended in this document, together with their units. Although this table includes most alternatives mentioned in the text, it cannot cover all of the points of detailed explanation and should be taken in conjunction with the text. Although for brevity and convenience all volumes are expressed in dm3, in all cases dm3 may be replaced identically with L or l (liter), and amount-of-substance concentrations may be expressed in M (molar), which is identical with mol dm-3. Both L and M may be used as primary units for forming multiples and submultiples such as mL,
Table 1. Recommended Symbols and their Units
![[tau]](../greek/TAU.GIF)
of a reaction is the time it takes for the extent of reaction to change by a proportion (
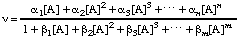. . . . . . . . (25)
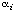in the numerator of the right-hand side of Eqn (25) has units (mol dm-3)1-i s-1, and any coefficient 
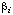in the denominator has units (mol-1 dm3)i. Similar equations are sometimes written in which the constant 1 in the denominator is replaced with a constant 
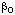. This practice is discouraged, because the equation then contains a redundant parameter and all of the coefficients 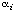, 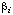have undefined dimensions. 
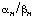with the meaning defined in Section 4.1. Moreover, it may also be useful to describe the kinetics quantitatively in terms of the slope of a plot of ![[mu]](../greek/MU.GIF)
M, etc.
| Symbol | Meaning | Customary unit | Section of text | See notes below |
|---|---|---|---|---|
| [A] | concentration of substrate A | mol dm-3 | 2.1 | 1, 2, 3 |
| [A]0.5 or [A]1/2 | value of [A] at which v = 0.5 V | mol dm-3 | 4.2 | 2 |
| [B] | concentration of substrate B | mol dm-3 | 2.1 | 1, 2, 3 |
| [E]0 (or [E]t or [E]stoich) | stoichiometric concentration of active centres | mol dm-3 | 4.1 | 1, 3 |
| h (or nH) | Hill coefficient | dimensionless | 10 | |
| [I] | concentration of inhibitor I | mol dm-3 | 6.2 | 1, 2, 3 |
| k | rate constant of any order n | (mol dm-3)1-n s-1 | 3 | 4 |
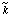| pH-independent value of k | as k | 8 | 5 |
| k app | apparent value of k | as k | 5.2, 6.4 | 5 |
| kA , kB | specificity constants for A, B | mol-1 dm3 s-1 | 4.1 | 2 |
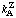 (etc.) | reciprocal Dalziel coefficient | (various) | 5.1 | 2 |
| kcat (or k0) | catalytic constant | s-1 | 4.1, 5.2 | |
| ki, k-i | forward and reverse rate constants respectively for ith step | as k | 3.1 | 4, 6 |
| Ki | inhibition constant (inhibition type unspecified) | mol dm-3 | 6.4 | |
| KiA | inhibition constant for A | mol dm-3 | 5.2 | |
| Kic | competitive inhibition constant | mol dm-3 | 6.4 | |
| kij | rate constant for step from Ei to Ej | as k | 3.1 | 4, 6 |
| Kiu | uncompetitive inhibition constant | mol dm-3 | 6.4 | |
| Km | Michaelis constant (or Michaelis concentration) | mol dm-3 | 4.2, 5.2 | |
| KmA | Michaelis constant for A | mol dm-3 | 4.2, 5.2 | 2 |
| Ks | substrate dissociation constant | mol dm-3 | 3.2 | |
| KsA | value of Ks for substrate A | mol dm-3 | 3.2 | 2 |
| k0 (or kcat) | catalytic constant | s-1 | 4.1, 5.2 | |
| nH (or h) | Hill coefficient | dimensionless | 10 | |
| [Q] | concentration of activator Q  | mol dm-3 | 7 | 1, 2, 3 |
| t | time | s | 2.1 | |
| v | rate (or velocity) of reaction | mol dm-3 s-1 | 2.2 | 7 |
| V (or Vmax) | limiting rate (or maximum rate, or maximum velocity) | mol dm-3 s-1 | 4.1, 5.2 | |
| vA | rate of consumption of A | mol dm-3 s-1 | 2.1 | 2 |
| vi, v-i, vij | chemical flux (or chemiflux) through step with rate constant ki, k-i, kij | mol dm3 s-1 | 3.1 | 4 |
| vmax | true maximum value of v | mol dm-3 s-1 | 4.1 | |
| vZ | rate of formation of Z | mol dm-3 s-1 | 2.1 | 2 |
| v0 | initial rate of reaction | mol dm-3 s-1 | 3.2 | 7 |
| [Y] | concentration of product Y | mol dm-3 | 2.1 | 1, 2, 3 |
| [Z] | concentration of product Z | mol dm-3 | 2.1 | 1, 2, 3 |
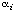| coefficient of [A]i in numerator of generalized rate expression | (mol dm-3)1-i s-1 | 10 | |
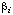| coefficient of [A]i in denominator of generalized rate expression | (mol-1 dm3)i | 10 | |
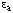| degree of activation | dimensionless | 7 | |
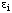| degree of inhibition | dimensionless | 6.3 | |
| relaxation time | s | 9 | |
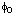 (etc.) | Dalziel coefficient | (various) | 5.1 | |
| for rate of reaction see Addendum 2 | 2.2 |
Notes:
1. Amount-of-substance concentration is abbreviated to concentration. This usage is acceptable in enzyme kinetics without special definition.
2. This symbolism can be extended to other reactants in an obvious way, e.g. KmX is the Michaelis constant of X.
3. Other ways of indicating concentration, such as a for the concentration of A, are acceptable but must be explicitly defined.
4. Any numbering of rate constants must be in explicit relation to a reaction scheme.
5. Other pH-independent or apparent values may be represented similarly. e.g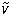 
is the pH-independent value of V.
6. The rate constants for the ith step of a reaction may alternatively be represented as k2i-1 and k2i instead of ki and k-i respectively (subject to note 4 above).
7. The initial rate may be represented by v, without subscript, when rates at other times are not in question. This rate is the steady-state rate extrapolated to zero time, not the true rate at zero time, which is normally undefined, because the rate of reaction is undefined during the transient phase of an enzyme-catalysed reaction.
1. International Union of Pure and Applied Chemistry and International Union of Biochemistry (1973) Enzyme Nomenclature, Recommendations 1972, Elsevier, Amsterdam.
2. Nomenclature Committee of the International Union of Biochemistry (1979) Enzyme Nomenclature, Recommendations 1978, Academic Press, New York.
3. International Union of Pure and Applied Chemistry (1981) Symbolism and terminology in chemical kinetics, 1980, Pure Appl. Chem. 53, 753 - 771.
4. International Union of Pure and Applied Chemistry (1979) Manual of Symbols and Terminology for Physicochemical Quantities and Units, Pergamon Press, Oxford; also in Pure Appl. Chem. 51, 1-41 (1979).
5. International Union of Pure and Applied Chemistry (1979) Glossary of terms used in physical organic chemistry (Gold, V., ed.) Pure Appl. Chem. 51, 1725-1801. [revised edition Pure Appl. Chem. 1994, 66, 1077-1184]
6. Nomenclature Committee of the International Union of Biochemistry (NC-IUB) Units of enzyme activity, Recommendations 1978, Eur. J. Biochem. 97, 319- 320 (1979) corrected 104, l (1980).
Addendum 1. Rate of conversion
From the JCBN NC-IUB Newsletter 1981 (see Arch. Biochem. Biophys., 1981, 206, 458-462; Eur. J. Biochem., 1981, 114, 1-4; Hoppe-Seyler's Z. Physiol. Chem., 1981, 362, I-IV; J. Biol. Chem., 1981, 256, 12-14.)
IUPAC has published recommendations [Pure Appl. Chem. 51, 1725-1801 (1979)] that the words 'rate of reaction' shall be the intensive quantity of dimensions (amount-of-substance concentration/time, i.e. units: mol l-1 s-1. This quantity is thus the rate of increase of concentration of product in systems of constant volume if one molecule of product is formed in the reaction equation. IUPAC had previously recommended that the name 'rate of reaction' should apply to the extensive quantity of dimensions: (amount of substance)/(time), i.e. units: mol s-1, now called 'rate of conversion'. NC-IUB welcomes the change, because biochemical usage has long been to name the intensive quantlty 'rate of reaction'.
Addendum 2. Rate of conversion Symbol
From Biochemical Nomenclature and Related Documents, 2nd edition, Portland Press, 1992 p 106.
The symbol for the rate of conversion, expressed in mol/s, is
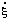
Return to home page for Enzyme Kinetics.